Project 2: Social Preferences Under Uncertainty and Ambiguity
Introduction
Consider a situation with \(n\) individuals where person \(i\) obtains a positive (desirable) outcome \(y_i\) and everyone's situation in society is summarized by the distribution of outcomes \((y_1,...,y_n).\)[1]
The main way in which evaluators in academic and policy circles often select among outcome distributions is by comparing their means. That is, if \((y_1(a),...,y_n(a))\) is the outcome distribution generated by treatment \(a\) and \((y_1(b),...,y_n(b))\) is the outcome distribution generated by treatment \(b\), the evaluator selects \(b\) over \(a\) whenever
\[ \frac{y_1(b)+...+y_n(b)}{n} > \frac{y_1(a)+...+y_n(a)}{n} \]While this is in many ways a sensible way to proceed, any such comparison of means is insensitive to the distribution of outcomes among the \(n\) individuals. It may very well be that treatment \(b\) leads to a large mean outcome solely on the basis of a few individuals enjoying very large outcomes, and accounting for this fact may reverse the evaluator's preferences between the treatments. In other words, despite \(b\) being more favorable than \(a\) in terms of mean outcomes, it is possible for an evaluator to prefer \(a\) over \(b\) overall if, despite it generating a lower mean outcome, treatment \(a\) generates very little inequality in the distribution of outcomes when compared to \(b\).
In general, we say that an evaluator is inequality averse when the evaluator prefers a perfectly equal society where everybody obtains outcome \(\bar{y}\) to a society with unequal outcomes \((y_1,...,y_n)\) and with mean \(\bar{y}\). To account for their attitudes towards inequality, inequality averse evaluators compare the distributions
\[ f(y_1(a)),...,f(y_n(a)) \]and
\[ f(y_1(b)),...,f(y_n(b)) \]in terms of their means for some continuous, strictly increasing and strictly concave function \(f\). In Protected Income and Inequality Aversion we learned how to identify what function \(f\) to employ on the basis of the tradeoffs between the outcomes of the different individuals that the evaluator considers acceptable and if you haven't read it yet I recommend that you do so at this point.
Adding Uncertainty and Ambiguity into the Analysis
Once the proper function \(f\) has been identified, one may be tempted to conduct the empirical analysis of treatments \(a\) and \(b\) by applying standard statistical and econometric tools to the distributions
\[ Y_1(a),...,Y_n(a) \]and
\[ Y_1(b),...,Y_n(b), \]where \(Y_i(a)=f(y_i(a))\) and \(Y_i(b)=f(y_i(b))\). One would then proceed in a “business as usual fashion”, namely, as though the evaluator is inequality neutral with respect to the transformed variables \(Y_i(a)\) and \(Y_i(b)\).
The key lesson of this project is that the proposed approach is suitable only when the evaluator faces no uncertainty or ambiguity about the distribution of outcomes associated with the treatments under consideration. However, when such uncertainty or ambiguity exists, a different approach is necessary to prevent the conflation of risk aversion and inequality aversion. This project seeks to identify and articulate the appropriate method for representing the evaluator's preferences over known outcome distributions, preserving the conceptual and analytical distinction between inequality aversion and risk aversion when uncertainty and ambiguity are present.
The technical details are in the paper (the draft of which is currently in preparation), and below I want to provide a couple of examples that illustrate the key problem the paper tries to solve, and how it solves it.
Illustration
Assume that the evaluator represents the uncertainty about what outcome distribution arises with a given treatment through a finite set of \(m\) states of the world, \(S = \{s_{1},...,s_{m}\}\). Treatment \(a\) is associated with an outcome distribution \(y^{s}(a)\) in state \(s\) and a prospect, \(y(a)\), collects the possible outcome distributions induced by treatment \(a\) across the \(m\) states. Therefore, one can think of \(y(a)\) as a matrix with \(m\) columns, \(y^1,...,y^m\), corresponding to the \(m\) possible outcome distributions induced by treatment \(a\). Similarly for treatment \(b\) and associated prospect \(y(b)\).
Consider now a situation with three individuals, two states of the world, and two prospects. Prospect \(y(a)\) is given by \(\left[\begin{smallmatrix} 4 & 2\\ 6 & 2\\ 5 & 2 \end{smallmatrix}\right]\) whereas Prospect \(y(b)\) is given by \(\left[\begin{smallmatrix} 3 & 1\\ 8 & 1\\ 10 & 1 \end{smallmatrix}\right]\), where rows correspond to individuals and columns corresponds to states.
To provide additional context to the example, you may imagine that treatment \(b\), if it works well (which happens in state 1), it generates a distribution of outcomes with a large mean and a large spread (of 3, 8 and 10), whereas if it does not work well (which happens in state 2), it generates a distribution of outcomes with no spread and very low outcome values (of 1 for each individual). In turn, if treatment \(a\) works well, it generates a distribution of outcomes with moderate mean and low spread (of 4, 5 and 6), whereas if it does not work well (which happens in state 2), it generates moderately low and equal outcomes (of 2 for each individual). One can think of treatment \(b\) as one that either works very well for almost everybody or not at all, and treatment \(a\) is a less extreme version of the same kind of policy.
Consider, in addition, an inequality averse evaluator with \(f\) given by the logarithm function. This means that, given a prospect \(y\), the evaluator computes, for each state \(s\), the magnitude \({\frac{1}{3}}(\ln y_1^s + \ln y_2^s + \ln y_3^s)\).
These computations are shown, for prospects \(y(a)\) and \(y(b)\), in the row labeled \(\mathrm{E}[\mathrm{log} \, y]\) in the table below:
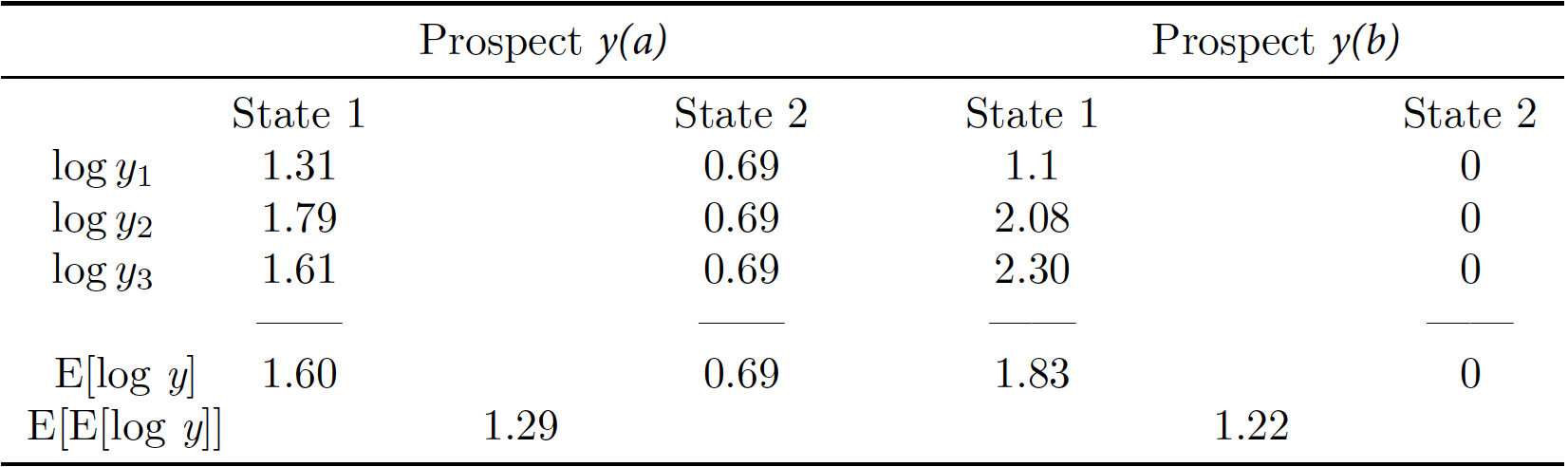
Assume further that the evaluator is a risk-neutral decision maker, with priors of \((\frac{2}{3},\frac{1}{3})\) on states 1 and 2 respectively.
This evaluator prefers prospect \(y(a)\) to prospect \(y(b)\), since the expected value of these (average) log measures is \(1.29\) for Prospect \(y(a)\) and \(1.22\) for Prospect \(y(b)\), as seen in the row labeled \(\mathrm{E}\big[\mathrm{E}[\mathrm{log} \, y]\big]\) in the table above.
However, an equivalent representation of those social preferences in any given state is the geometric mean of outcomes. Say we were to use this representation. This means that, given a prospect \(y\), the evaluator would compute, for each state \(s\), the magnitude \((y_1^s y_2^s y_3^s)^{\frac{1}{3}}\), shown in the row labeled \(\mathrm{GM}[y]\) in the table below, and the expected value of these geometric mean measures is then \(3.95\) for prospect \(y(a)\) and \(4.48\) for prospect \(y(b)\), shown in the row labeled \(\mathrm{E}\big[\mathrm{GM}[y]\big]\) in the table below. According to this, the evaluator prefers prospect \(y(b)\) to prospect \(y(a)\).
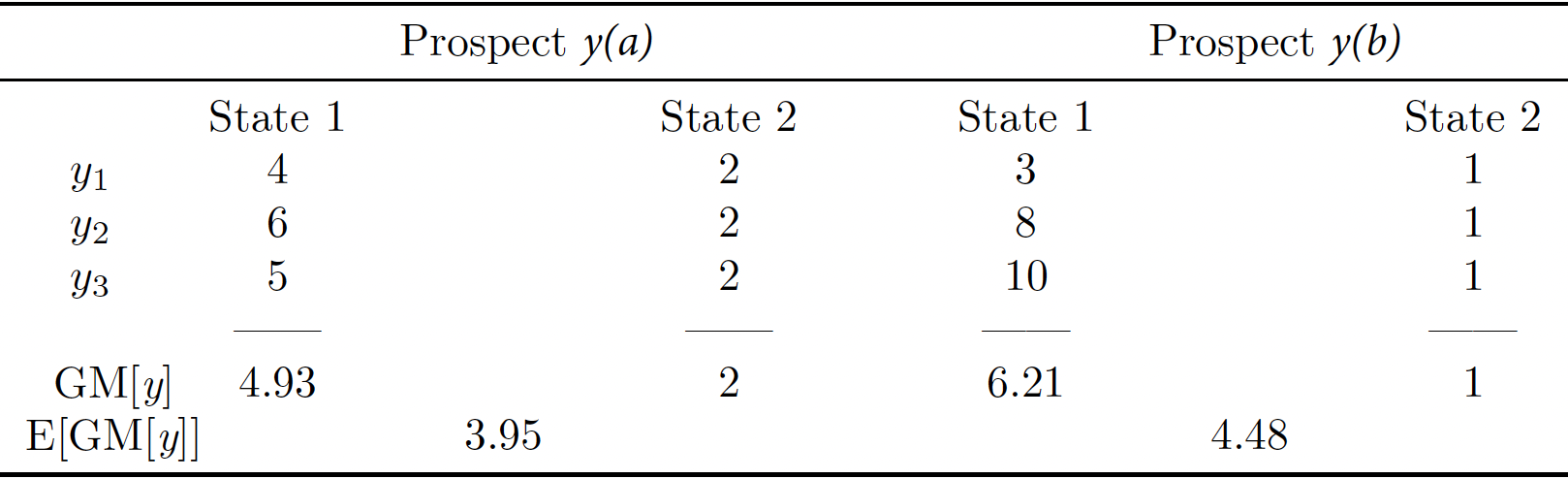
We then have two representations of the evaluator's social preference over known outcome distributions. They are equivalent in the sense that they both correctly represent the social preference over known income distributions. However, once we add uncertainty and ambiguity about what outcome distribution arises with a given treatment, their recommendations as to which is the preferred treatment differ. The question is: which of these representations, if any, is giving the right answer?
In order to properly investigate this question, we need to introduce an additional concept, first developed in Atkinson 1970.
Egalitarian Equivalent
The egalitarian equivalent[2] \(ee = \mathcal{EE}(y_1,...,y_n)\) of a distribution of outcomes \((y_1,...,y_n)\) is the outcome level \(ee = \mathcal{EE}(y_1,...,y_n)\) such that, the evaluator would be indifferent between the distribution \((y_1,...,y_n)\) and \((\underbrace{ee,..., ee}_{n-times})\). The egalitarian equivalent is therefore computed as follows:
\[ \mathcal{EE}(y_1,...,y_n):=f^{-1}\left(\frac{f(y_1)+...+f(y_n)}{n}\right). \]For an inequality averse evaluator the following is true:
\[ \mathcal{EE}(y_1,...,y_n) < \frac{y_1+...+y_n}{n}. \]The Main Result
Theorem 3.1 in Social Preferences Under Uncertainty and Ambiguity, following Fleurbaey 2010, shows that the following is true:[3]
If, in the absence of inequality, the evaluator acts as though there is only one (representative) individual then, in the presence of both inequality and uncertainty, the evaluator chooses among treatments by comparing the profiles \((\mathcal{EE}(y^1),...,\mathcal{EE}(y^m))\) among treatments using their preferred single-person decision problem evaluation framework.
Interpretation and Implications
Under the assumptions of this theorem, the social evaluation can be done as the single-person evaluation, but one applies the single-person decision methodology under uncertainty or ambiguity to the profile of egalitarian equivalent measures \((\mathcal{EE}(y^1),...,\mathcal{EE}(y^m))\). Therefore, given a social preference about known outcome distributions in society, one incorporates those into a treatment evaluation framework under uncertainty and ambiguity, given a set of states of the world, by first aggregating across individuals for each state, using the egalitarian equivalent representation of the social preferences under certainty, and then aggregating across states in whichever way the evaluator normally does so in single-person decision problems under uncertainty or ambiguity.
This is significant because, as the example above shows, the choice of representation of the evaluator's preferences can be consequential in cases with statistical uncertainty: one would obtain different rankings over treatments depending on what representation one was using. After aggregating across states, \(y(a)\) ranks above \(y(b)\) according to \(\mathrm{E}\big[\mathrm{E}[\mathrm{log} \, y]\big]\), and \(y(b)\) ranks above \(y(a)\) according to \(\mathrm{E}\big[\mathrm{GM}[y]\big]\). Which representation one uses ends up making a difference for the analysis under uncertainty and ambiguity. Among these, we will prefer the measure based on \(\mathrm{GM}[y]\)because that is the one that does not conflate risk aversion and inequality aversion.
Inequality Aversion \(\ne\) Risk Aversion
When contemplating which representation of the social preferences under certainty to incorporate into one's statistical framework, it bears noticing that using the \(\mathrm{E}[\mathrm{log} \, y]\) representation amounts to imputing a degree of risk aversion to the evaluation that the evaluator does not necessarily have. This can be seen most easily in the case of a risk-neutral evaluator in an evaluation where there is no inequality. In this case, using the \(\mathrm{E}[\mathrm{log} \, y]\) representation amounts to applying a concave transformation of the data coming from the representative individual before taking expectations across states, and this would make the decision maker act as though they are risk averse, even if they are not. The \(\mathrm{GM}[y]\) representation, on the other hand, makes no such imputation.
Let's illustrate this finding through a variant of the previous example:
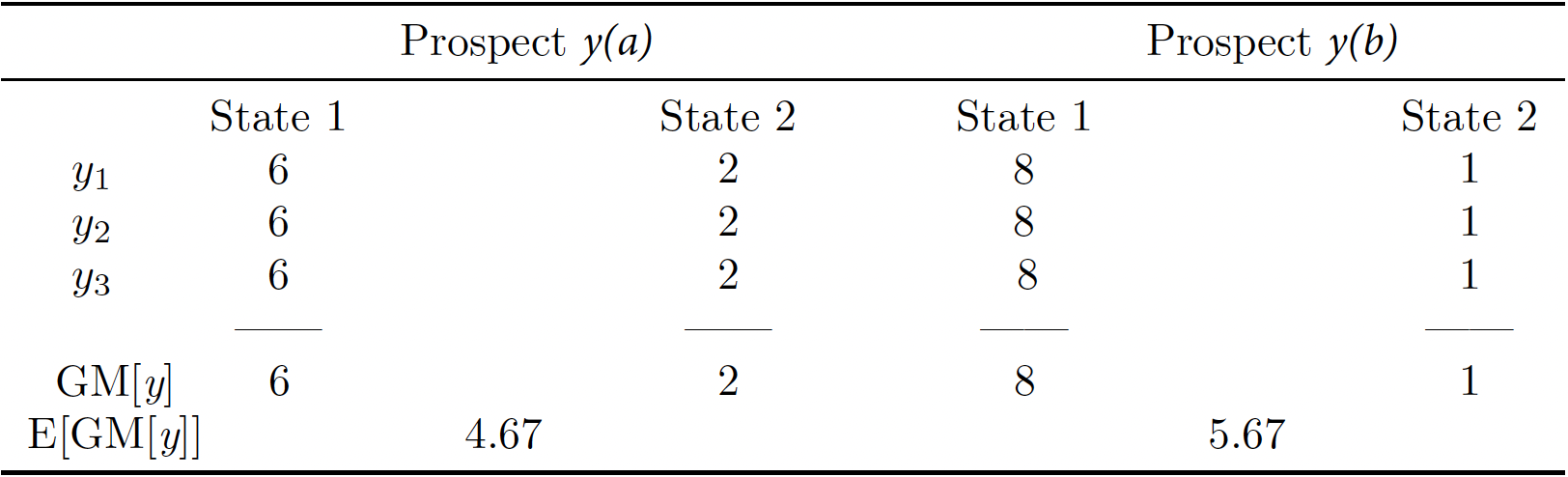
In this variant, there is no inequality but there is uncertainty. With this decision maker being risk neutral, the comparision between treatments then boils down to assessing which is better: \(y(a)\), which yields \(6\) with probability \(\frac{2}{3}\) and \(2\) with probability \(\frac{1}{3}\) for the representative individual, with expected outcome \(4.67\), versus \(y(b)\), which yields \(8\) with probability \(\frac{2}{3}\) and \(1\) with probability \(\frac{1}{3}\) for the representative individual, with expected outcome \(5.67\). The expected outcome is larger for \(y(b)\), and therefore \(y(b)\) would be the prospect chosen.
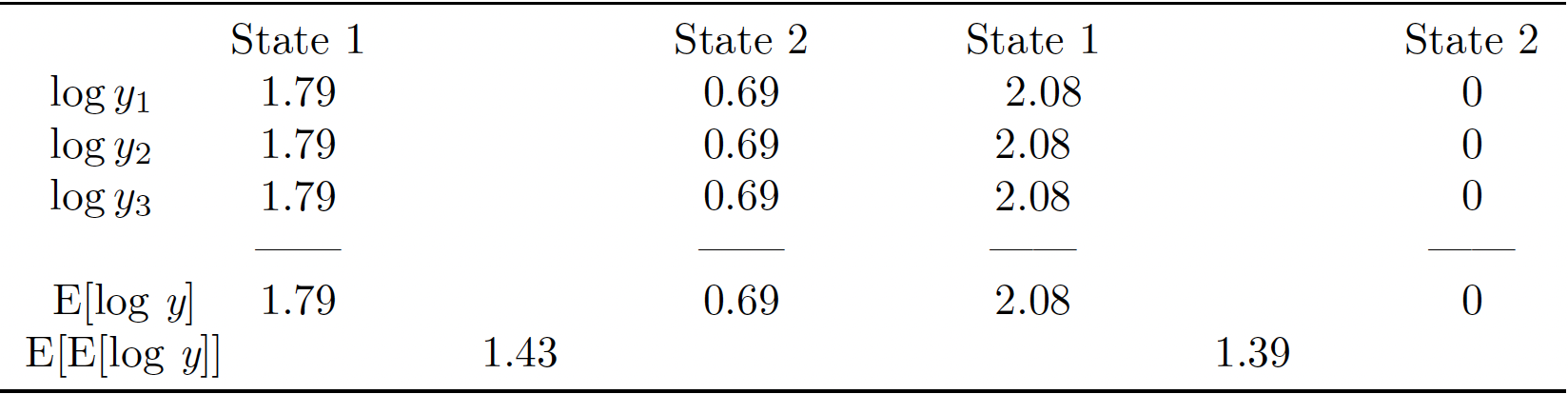
This is not what happens when analizing the example under the \(\mathrm{E}[\mathrm{log} \, y]\) representation of the social preferences under certainty: the evaluator would end up comparing \(y(a)\), with expected log measure \(1.43\), to \(y(b)\), with expected log measure \(1.39\), and conclude that \(y(a)\) is better. This is the conclusion that one would reach if the evaluator was analizing the situation of a single representative individual and was risk averse, with Bernoulli utility function given by the logarithm function. Our evaluator in this example is not risk averse, however, yet the \(\mathrm{E}[\mathrm{log} \, y]\) representation of the evaluator's social preferences under certainty is unwittingly making such imputation. One avoids this problem in this example by using the \(\mathrm{GM}[y]\) representation instead, and the reason why this works is that \(\mathrm{GM}[y]\) is in fact the way one computes the egalitarian equivalent of \(y\) for an evaluator that has \(f\) as the logarithm function in a social evaluation problem under certainty.
Next Steps
The third project in this series extends the optimal treatment choice apparatus described in Manski 2024 to the case where the welfare evaluation is made using the egalitarian equivalent measures described above, and explore the optimal treatment rules that arise. I investigate egalitarian equivalent optimal statistical decisions for the Bayesian, maximin, and minimax regret evaluators. We will learn that when the true state is point identified, the subtlety discussed above about what representation of the social preferences under certainty one should bring into the statistical decision analysis does not arise, but the situation is different under partial identification. In this case, the optimal treatment assignment depends on the chosen representation of social preferences under certainty. This paper emphasizes that the egalitarian equivalent representation is the most appropriate to incorporate into a statistical framework, provided the assumptions behind Theorem 3.1 in Social Preferences Under Uncertainty and Ambiguity are deemed acceptable.
Endnotes
| [1] | This project considers any outcome of interest as an index of individual advantage, but the results extend immediately to any cardinal, interpersonally comparable variable. In particular, it is possible to adjust the outcome for other aspects of quality of life that individuals enjoy or endure, and use this adjusted outcome as the relevant index instead of the ordinary outcome. |
| [2] | Also known as equally distributed equivalent. |
| [3] | Under standard continuity, dominance, and Pareto conditions. |
